This is the second chapter about sun.
We are talking more and more about renewable energies, where solar panel is one possible option. However, the productivity depends on the current latitude, the day and the current time (which governs \(\alpha\)). If not oriented correctly, the energetical yield is not maximal.
Computing the yield at a given date-time is easy. Take a look at the following figure:
The figure above represents a solar panel put flat on the ground. You can see that the “sun surface”, in orange, is much smaller than the solar panel surface. The yield is simply this surface ratio.
This yield can be computed for a given \(\alpha\), assuming the panel is facing the sun (i.e., oriented on the ground according to \(HRA(t)\)). This yield is:
\[R(0°, t, Lat, N) = \sin(\alpha(t; Lat, N))\]Suppose we are located near Paris (latitude 48.52°), and we look at the yield at noon.
Then \(\alpha\) is maximal in summer (around 63°) while minimal in winter (around 19°).
Because this angle changes day after day, a fixed solar panel cannot give the maximal yield of 100 % every day.
If we compute the ratio, we have a ratio of 90 % in summer while only of 35 % in winter.
The difference is huge !
In the previous paragraph, we compared two yields at noon. However, noon is just a small time-frame during the day. To optimize the global yield, we have to find the orientation that maximize it all the day long.
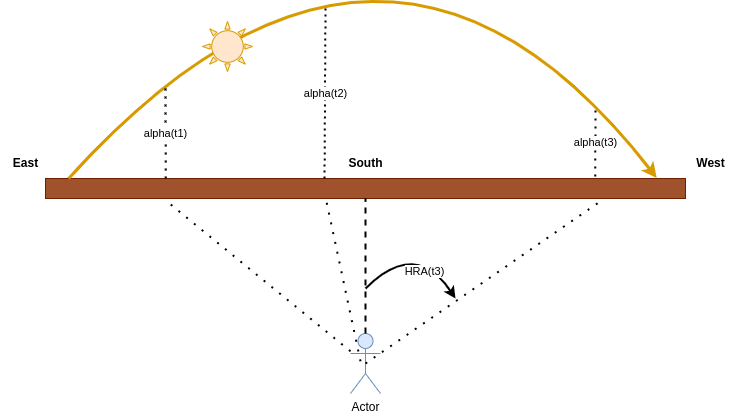
To optimize the yield, we first need to understand that \(\alpha\) is a 3D angle: it is the angle between the sun, our position, and the closest location in the horizon.
Therefore, to obtain the maximal yield of 100 %, we need to play on two components:
To optimize the rotation angle of the solar panel, we just need to follow the \(HRA(t)\) angle, by turning the solar panel at a speed of 15° / hour so the panel is always facing the sun.
For the inclination angle, looking back at the previous figure, we need to get the solar panel perpendicular to the sun rays. In other words:
\[\text{Inclination}(h, N, lat) = 90° - \alpha(h, N, lat) = y\]where \(\text{Inclination}\) is the angle of the solar panel relatively to the ground, also called the tilt angle.
Because the sun moves constantly, these two angles need to be adjusted every minutes. The best possible option is to add two motors to follow the sun.
However, this option is not always possible:
In these cases, you need to choose the best orientation angles which maximize your yield.
If you cannot move your panel (or very infrequently), you have first to define clearly the usage of this panel:
If you are selling your electricity to the network, you prefer to maximize the global yield if you have a flat price. There are already online calculators 2 that gives you this optimal angle.
But if it is for personal use, you are likely to use more electricity in winter (for heating, for preparing food) than in summer (where you prefer to eat salads).
Because the yield is not a linear function, the tilt angle is not \(90° - \bar{\alpha}\) (where \(\bar{\alpha}\) is the average value of \(\alpha\)).
If you can at least add a motor to rotate your panel on the ground at a constant speed, you can already have a good yield. We will move progressively from:
The yield hour after hour is just the instantaneous yield:
\[\text{Yield}(t, N, lat, \beta) = \sin(\beta + \alpha(t, N, lat))\]When changing the tilt angle, you can see “jumps”, as moving your panel doesn’t help to rise the sun earlier.
To get the average yield over a day, we need to integrate over the daytime.
\[\text{Yield}(N, lat, \beta) = \frac{1}{t_{set} - t_{rise}}\int_{t_{rise}}^{t_{set}} \text{Yield}(t, N, lat, \beta) \,dt\]Daytime is longer in summer, and shorter in summer. Here, we normalize by the daytime to compare the average yield. Nevertheless, we have to keep in mind that all days do not have the same importance.
You may seem that there is a glitch for high latitude in winter (>70°), when the yield move from 100% to 0%.
This is because there is no “day”, the sun does not rise, even for one minute.
As this plot is the average yield over daytime (not over 24 hours), this might be misleading.
As discussed previously, days are shorter in winter and longer in summer. If we compute the yield relatively to one day, we get the “true” yield.
\[\text{Yield}^*(N, lat, \beta) = \frac{1}{24}\int_{t_{rise}}^{t_{set}} \text{Yield}(t, N, lat, \beta) \,dt\]When we have a photovoltaic solar panel, the goal is to maximize the yield over the year if we sell electricity. Therefore, we are interested by the angle that maximize this value.
\[\text{Yield}^*(lat, \beta) = \frac{2}{24 \times 365}\int_{365}^{0}\int_{t_{rise}}^{t_{set}} \text{Yield}(t, N, lat, \beta) \,dt\,dN\]Here we multiply by \(2\) as there are \(12\) hours in average in a day. This value is more realistic, as it corresponds to the best possible yield given the total daytime.
What you can see is that even you have a fixed tilt angle, this is not that bad.
If you selected the optimal orientation, if you can turn your panel, yields are above 80%, without the need to be precise on the tilt angle.
When you cannot turn your panel over the day, the best rotation angle is facing south (unless you are in a mountain). For the tilt angle, there are many online calculator 3, 4. Because \(\alpha\) varies between \([0, \alpha_{max}]\), a rule of thumb is to select the tilt angle in between. In some websites, they recommend \(\beta \approx 90 - (\alpha - 10)\), where \(\alpha\) is the value at noon in summer, as you have longer daytime.
The solar panel with tilt angle \(\beta\) and sides of length \(a\) and \(b\) can be described by \(4\) points: \(i=(0, 0, 0)\), \(j=(0, a, 0)\), \(k=(b\cos\beta, a, b\sin \beta)\), and \(\ell=(b\cos\beta, 0, b\sin\beta)\).
One vector perpendicular to the solar panel is \((-\tan (\beta), 0, 1)\).
The sun rays have an angle \(\alpha\) over the z-axis, and an angle \(HRA\) within the \((x, y)\) plane.
One vector perpendicular to the sun plane is \(\overrightarrow{v_{sun}} = (\cos(HRA), -\sin(HRA), - \tan(\alpha))\). The equation of this plane is \(x\cos(HRA) - y\sin(HRA) - z\tan(\alpha) = 0\).
We want to compute the image of all points of the solar panel within the sun plane. In other words, we want to find \(\lambda\) such as:
\[j' = j + \lambda \overrightarrow{v_{sun}}\]and \(j'\) is in the sun plane. For a point in the panel plan \((x, y, z)\), the corresponding \(\lambda\) is:
\[\lambda = \frac{-x \cos(HRA) + y \sin(HRA) + z\tan(\alpha)}{1 + \tan^2(\alpha)}\]For simplicity of the equation, we denote \(X = 1 + \tan^2(\alpha)\) and \(Y= \sin(\beta) \tan(\alpha) - \cos(\beta)\cos(HRA)\)
The image of \(i\) is itself. The image of \(j\) is \(j'=a(\frac{\cos(HRA)\sin(HRA)}{X}, 1 - \frac{\sin^2(HRA)}{X}, - \frac{\tan(\alpha)\sin(HRA)}{X})\). The image of \(\ell\) is \(\ell'= b(\cos(\beta) + \frac{Y\cos(HRA)}{X}, -\frac{\sin(HRA) Y}{X}, \sin(\beta) - \frac{\tan(\alpha)Y}{X})\).
The area of the parallelogram \((i', j', k', \ell')\) can be expressed as:
\[\mathcal{A} = \sqrt{1 - \left(\frac{\overrightarrow{ij}.\overrightarrow{i\ell}}{\|\overrightarrow{ij}\|\|\overrightarrow{i\ell}\|}\right)^2}\times \|\overrightarrow{ij}\|\|\overrightarrow{i\ell}\|\] \[\|\overrightarrow{ij}\| = a\sqrt{1 - \frac{\sin^2(HRA)}{X}}\] \[\|\overrightarrow{i\ell}\| = b\sqrt{1 - \frac{Y^2}{X}}\] \[\overrightarrow{ij}.\overrightarrow{i\ell} = -ab\frac{\sin(HRA)Y}{X}\]To get the yield, we need to divide the area by the solar panel surface \(a\times b\).
On the next figure, you can explore the yield as a function of time.
The best yield are concentrated near noon, and sharply drop for the rest of the day. If the panel is well oriented, the yield in winter is as good as in summer, as all the production is made around noon in both cases.
With a non-moving panel, you can see how the yield is affected.
In the best best cases, you get a yield of 40% in summer, and 30% in winter (over 24 hours).
Compare to the 60% in summer and 40% in winter when you can rotate your panel, you have a drop of -33% of efficiency, which is a lot.
If you plan/have a thermal solar panel (for heating water), it is more interesting to use winter optimal tilt angle: you may prefer to take a hot bath in winter than in summer when it is 30°C outside !
If you have a 2-axis rotative solar panel, you can get 100 % yield all the day long.
However, this is for one panel.
If you have several solar panels, you need to space them appropriately, otherwise their shadows may reduce the yield.
When the sun is high or/and when the panels have a low tilt angle, there is no shade. There is even land that receive sunlight.
When panel are optimally oriented and sufficiently spaced, they can all reach the maximal yield.
But when the sun is too low, or if there isn’t enough space between the panels,
the first one in the row can reach the 100 % yield, but not the others.
You have a trade-off between available land, the number of solar panels, and the total electricity production.
To space correctly the panel, to avoid shading, the distance between panels (the distance from left edge of panel i to left edge of panel i+1), for a panel of length \(D\) is:
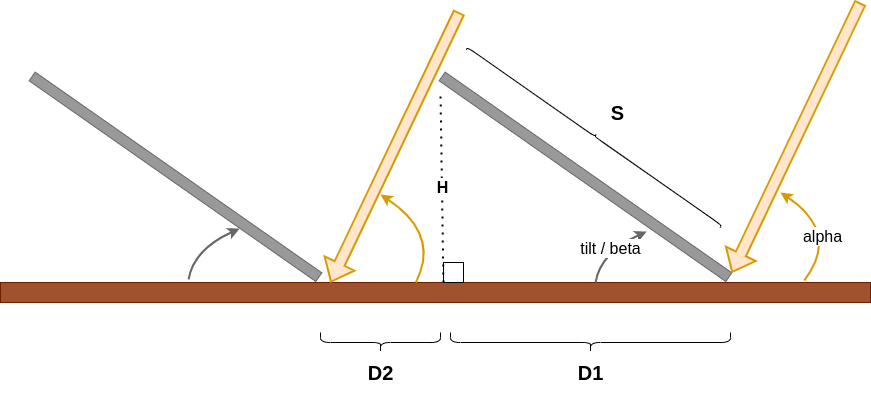
Therefore, the total distance \(D=D_1 + D_2\) between solar panels is:
\[D = S \left[\cos(\beta) + \frac{\sin(\beta)}{\tan(\alpha^{min})}\right]\]where \(\alpha\) is the minimal sun angle we want to capture.
In theory, \(\alpha^{min}\) is minimal at sunrise and sunset, with a value of 0°.
However, this leads to infinite distance between panels, which is not the best strategy to cover an area.
And next, we have to consider the environment: relief, trees, building, which will prevent from seeing the sun until it reaches some specific \(\alpha\).
Unless you are on the top of a mountain, this angle is greater than \(0\).
Also, if your panel has a fixed angle, yield when sun has a low elevation angle is low, so this worst case is not that impacting. In any case, if you want to build a farm of solar panel, you need to have access to each of them, in case of maintenance.
This is a simple simulator, where you can play on the panel size, and angles. Given the minimal angle you want capturing energy, you can design your system by spacing sufficiently the panels.
For very small angles (lower than 20°), you can see that the shade goes very far away.
For an angle of 30° (\(sin(30°) = 0.5\)), the size of the shade is equal to the area occupied by the solar panel.
In this blog post, we presented the theoretical yields of a solar panel. We made the assumption that the tilt angle was fixed, but we can rotate it. Even if the tilt angle is not very precise, just following the sun over the day is enough to get a good yield.
Nevertheless, for making a solar panel farm, we have to consider the shade made by solar panels on the others. This require a non-negligible space between solar panels.
In the next post, we will look at “true” or “real life” solar panels. You can go by clicking here:
III: True solar panel efficiency
>> You can subscribe to my mailing list here for a monthly update. <<