
After reading the book Rainwater Harvesting, vol. 1, 2013, Brad Lancaster(chapter 4, page 138), I wanted to know a little bit more about sun trajectories. In this book, the author discussed low-cost solutions for taking advantage of sunlight, especially in summer where temperatures are too hot:
These strategies are highly linked to the sun trajectories. Therefore, I wanted to understand how we can calculate them and exploit this knowledge.
I have some personal interests in understanding what is the optimal orientation of solar panels (for drying fruits). About solar panels, I wanted to look at yields and true yields (i.e. yield in real conditions), to see what is the margin of progress if we turn the panel all the day long.
There are plenty of website making great course about earth ellipse. Here, I present the basic, and propose a tree shade simulator, for computing the optimal distance between the tree and a house.
Series:
A short course about earth angles
As said previously, we will just illustrate with simple figures what is what.
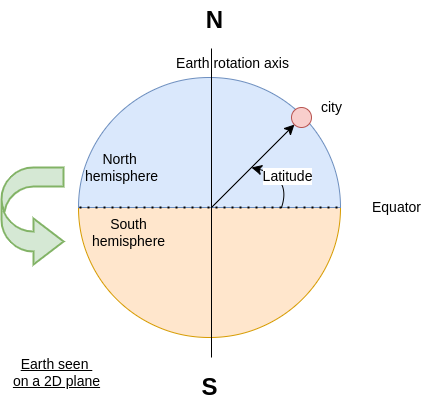
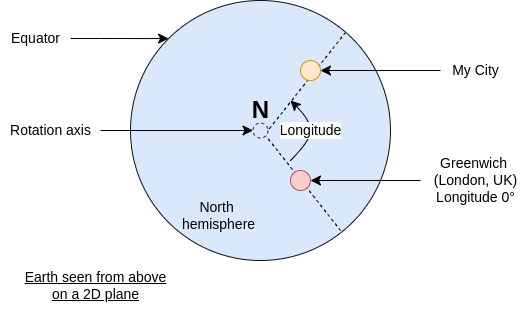
“North” and “South” are true location. This is where the earth axis “edges” are located. When you are at the northernmost point, you cannot go north anymore.
While “East” and “West” are relative:
\[\text{Europe} \xrightarrow{east} \text{Russia} \xrightarrow{east} \text{Japan} \xrightarrow{east} \text{Mexico} \xrightarrow{east} \text{Europe}\]Nevertheless, longitude is measured with respect to Greenwich location, so we have a single way to measure it: x° left or right from Greenwich.
To give you an idea of the typical latitude, here is a list of several capitals in the north hemisphere and their associated latitude.
You can find your own latitude for instance there.
| Country | City | Latitude |
|---|---|---|
| Norway | Oslo | 59.9138688 |
| Russia | Moscou | 55.7508 |
| Netherlands | Amsterdam | 52.37 N |
| UK | Londres | 51.509093 |
| Belgium | Bruxelles | 50.850340 |
| France | Paris | 48°52N |
| Switzerland | Zurich | 47.3686498 |
| Canada | Ottawa | 45.4215296 |
| Espagna | Madrid | 40.38 N |
| US | New York | 40° 46′ 47.629″ |
| China | Pekin | 39°54’20” N |
| Japan | Tokyo | 35.6894 N |
| Morocco | Morocco | 31.17282 N |
You can see that the units in the table are not all the same.
There are two usual notations: floating degree (xy.abcd) and “time” degree (xy° mn' ps").
It is easy to convert degrees / minutes / seconds into the floating degree format, which is much more convenient for computation:
\[angle = deg + \frac{min (')}{60} + \frac{sec (")}{60^2}\]The Earth turns around itself, which leads to day and night.
The Earth turns around the sun on an ellipse1, but it’s almost a circle (the closest position is 147 millions km away in january, while the furthest is 152 millions km in July).
This difference doesn’t explain seasonality.
The factor that explain the seasons and daytime change is the earth axis inclination against the Sun-Earth ellipse, which is of 25°26'11" = 25.4363889°.
Because of the earth axis angle, the sun angle changes over time, and is specific to a given location.
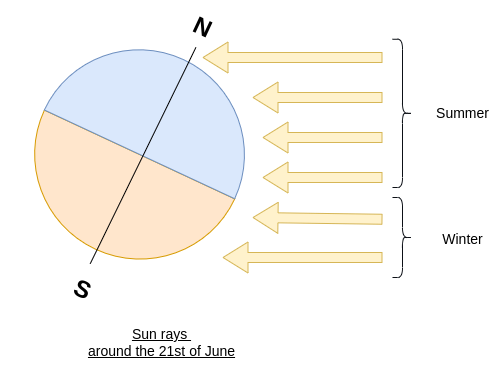
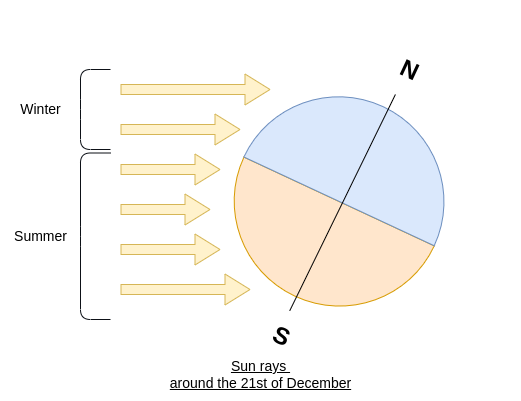
In these figures, the drawn rays are parallel and equidistant. In winter, because of the angle, the surface covered by one ray is larger than in summer. We have a lower ratio \(\frac{\text{Surface(Ray)}}{\text{Surface(Soil)}}\), leading to a lower amount of energy per area compared to summer.
There are formulas to calculate the current angle between the Earth and the Sun. The two main angles are:
These two angles are complementary, i.e.:
\[90° = \text{Zenith} + \text{Elevation}\]The elevation angle is more intuitive, as \(0\) (or a low angle) is associated to the sun rises or sets, the horizontal position.
To compute this value, there is a simple formula, which is:
\[\delta(N) = -23.44° \cos\left(\frac{N+10}{365} \times 360 \right)\]where:
21st of December.x 360 is to convert the ratio into an angle in degree-23.44° is the earth inclination angle (rounded).The declination angle \(\delta(N)\) is the angle of the sun relative to the equator. Because the sun is far away from the earth, the sun rays can be considered as parallel all over the earth.
As the earth is a sphere, the sun rays are seen with a different angle, therefore we see different sun trajectories This is where we introduce the elevation 2 angle \(\alpha\), which is the declination angle relatively to the current position.
The three angles are linked, and we can easily compute the elevation angle given a latitude and the current day:
\[\alpha^*(N, lat) = 90° + lat - \delta(N)\]This value correspond to the maximal angle between the sun and the earth during a day on a current location. Generally, it occurs around noon, but often the solar time is different from the local time. In general, to have the sunrise near 7 a.m., and sunsets near 9 p.m., the solar noon occurs at 2 p.m.
Last, we need to talk about time equation 3. When we compute the elevation angle, we suppose that the current longitude is in the (earth axis, Sun) plane. Which is true for less than one second in a day. We need to take into account the angle between the current location and this plane.
The earth makes one turn every 24 hours (not exactly, but this is a good approximation).
Therefore, its rotation speed (degrees per hour) is:
The hour angle (HRA) is just the angle relatively to the solar mid-day.
\[HRA(t) = \omega(t - 12)\]where \(t\) is the local solar time (in hour), i.e. the true time relatively to the sun in our position. With this angle and the previous ones, the declination angle is extended into:
\[\alpha(t, N, lat) = \sin^{-1}\left(\sin(\delta)\sin(lat) + \cos(\delta)\cos(lat)\cos(HRA(t)) \right)\]To obtain this equation, you need to work with 3D angles equation. We skip the details to obtain it.
Now, as we have the equation, we can play with a little bit. Here is a simulator for the north hemisphere (for the south, just shit the days by 180). As I don’t know your time zone, the time is of course the solar time, which need to be corrected for your needs.
Because the slider is in terms of day, here is a table to get an idea of \(N\) every first of the month:
| Month | \(N\) | Month | \(N\) | |
|---|---|---|---|---|
| \(1^{st}\) of January | 0 | \(1^{st}\) of July | 181 | |
| \(1^{st}\) of February | 31 | \(1^{st}\) of August | 212 | |
| \(1^{st}\) of March | 59 (-1) | \(1^{st}\) of September | 243 | |
| \(1^{st}\) of April | 90 | \(1^{st}\) of October | 273 | |
| \(1^{st}\) of May | 120 | \(1^{st}\) of November | 304 | |
| \(1^{st}\) of June | 151 | \(1^{st}\) of December | 335 |
You can test for high latitudes (above 70°):
If you are in the south hemisphere, you need to add \(\frac{365}{2}=182.5\) to these dates so we are upside down.
You can also check more advanced tools here 4.
You can get access to the next post of this series here:
II: Solar panel orientation and yield
>> You can subscribe to my mailing list here for a monthly update. <<