
Versailles’s floor is a puzzle: many pieces to assemble together. I wanted to create a simple simulator for the most common pattern.
This is a simple javascript simulator, made with Bokeh.
You can play with using two sliders:
R slider modifies the trade-off between the square and the lines (of lenght a and b respectively).length slider doesn’t change anything visual, this is only if you don’t want to compute the size of the pieces yourself. The length represents the total length (borders included).We will first forget about the total length. The reference unit will be R, the ratio between the large squares, and the spacing rectangles.
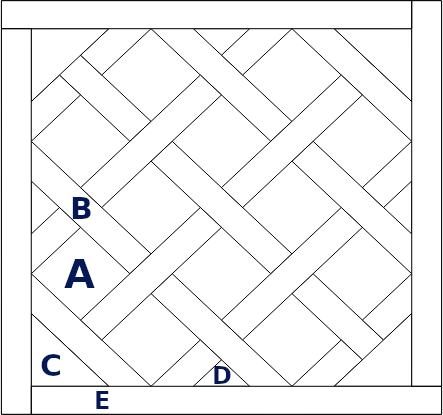
Edge of A:
Width of B:
from which you get the diagonal:
\[D_a = \sqrt{2 \times a^2}\] \[D_b = \sqrt{2 \times b^2}\]For the rectangle B, \(D_b\) is not the diagonal: it is the length of the smallest edge cut with an angle of 45°.
Diagonal of the angle’s triangle C:
From which you get the side of the triangle:
\[y = \sqrt{\frac{x^2}{2}}\]For the small triangle D, the hypotenuse is:
The internal length (not the total one) is:
\[L = 2 \times y + 4 \times D_b + z\]This is the length of a border E (and \(b\) is the width).
If we want to move from our unit defined as the length of two main elements glued together to the total size of a pannel, this is easy.
To convert all the previous numbers into the target unit, we just need to compute:
\[w' = w \times \frac{L_0}{L + 2 \times b}\]where \(w\) is the length to convert and \(w'\) the resulting value.
Well, you need to find the coordinate of B rectangles.
Next, the simplest is to perform translation (horizontal and vertical) of \(D_a + D_b\).
There are rectangles that are cut at 45°.
To avoid finding the coordinates, the simplest thing to do (from a computer science perspective) is to add above these B rectangles the borders E. So they hide the edges.
>> You can subscribe to my mailing list here for a monthly update. <<