
Il est beaucoup plus aisé de s’intéresser aux choses que l’on peut voir, toucher et sentir facilement. En revanche, tout ce qui est invisible et impalpable, cela devient beaucoup plus dur.
On tend à nous éduquer à ces choses qui sont dans l’air:
Tous ces éléments sont importants à considérer, mais il y a une autre molécule, bien plus importante, tant bien quantitativement que son impact est important sur nous: l’eau.
Trop humide, et le linge ne sèche jamais, de la moisissure apparaît sur nos murs, ce qui impacte la qualité de l’air. Trop sec, et les meubles en bois se fissurent, et on se déshydrate plus rapidement.
En ces temps où l’on nous parle d’économie d’énergie, d’isolation thermique des habitats, on nous en parle sans nous en parler. Le confort d’une maison est fonction de sa température, mais aussi de son humidité qui impacte énormément le ressenti. Lors de travaux de rénovation, l’aération est le composant principal pour jouer sur le paramètre humidité.
L’idée de cette article est de présenter les différentes lois de chimie qui permettent de calculer la quantité d’eau dans l’air en fonction de la température, pour avoir des ordres de grandeur. La deuxième partie prendra pour exemple des cas concrets dans la vie de tous les jours pour optimiser l’énergie et le temps dépensés.
On ne peut expliquer les différents phénomènes liées à l’eau avec une seule loi. Trois principales permettent de comprendre son comportement:
Avec ces différentes lois, on peut estimer les quantités d’eau dans l’air pour nos applications.
Une des lois les plus élémentaires en chimie est la loi des gaz parfaits:
\[PV = nRT\]où:
Cette loi est assez intuitive:
Les “vrais” gaz parfaits sont les gaz des éléments du tableau périodique de la dernière colonne: Hélium, Argon, Neon, Krypton, … Donc très peu de molécules rentrent dans cette catégorie. Ces atomes ont la particularité d’avoir leurs orbitales atomiques pleines d’électrons, et ne sont donc pas disposés à interagir avec d’autres molécules.
» Liens vers le tableau périodique des éléments. «
Les autres atomes et molécules sous forme gazeuse ne sont donc pas des gaz parfaits. Néanmoins, on peut faire des approximations. Un gaz parfait a la caractéristique que ces composants n’interagissent pas entre eux. Dans certaines conditions, on peut considérer un gaz non-parfait comme parfait, en disant que les molécules intéragissent peu, et que ces interactions sont alors négligeable. Autrement, il faut rajouter des termes correcteurs à cette première loi.
Il y a deux conditions principales:
Sur notre plage “humaine” (\(P = 1\) bar, \(T \in [0 - 100] °C\)), ces hypothèses sont valables. Aussi, le but de cette article est de donner des ordres de grandeurs, et non pas de faire des calculs exacts, nous négligeront donc les variations qui existent.
Une seconde loi qui est assez intuitive est la loi de Dalton, qui fait la relation entre pression totale $P$ et pression partielle des éléments:
\[P = \sum_i P_i\]Ou en inversant:
\[P_i = x_i P\]où \(x_i \in [0, 1]\) est la fraction molaire du composé $i$.
Avec l’image de la voiture, le poids de la voiture est proportionnel à ce que vous mettez dedans: 1 valise + 2 sacs + 1 glacière + 3 personnes. La seule chose qui faut garder à l’esprit est que $P$ et $P_i$ ne dépendent pas du poids des éléments, mais de leur nombre ($n$). D’une certaine manière, une unité de personne est équivalent à une unité glacière, ce qui peut être contre-intuitif pour le coup.
Dans l’air que nous respirons, il y a environ 78% de \(N_2\) et 21% de \(O_2\), et le reste un mélange d’autres gaz. Ces pourcentages sont molaires. Une mole de diazote (\(N_2\)) a une masse de \(2 M_{N_2} = 2 \times 14 = 28 g.mol^{-1}\), tandis que celle de dioxygène \(O_2$ de $2 M_{O_2} = 2 \times 16 = 32 g.mol^{-1}\). La différence n’est pas très grande entre ces deux molécules, mais cela a son importance.
On peut ainsi obtenir la masse d’oxygène dans $1m^3$:
\[m_{H_2O} = M_{H_2O} n_{H_20} = M_{H_2O} \frac{P_{H_20} V}{R T} = M_{H_2O} \frac{0.21 P V}{R T}\]En remplaçant par des valeurs numériques, on obtient pour \(1m^3\) à \(20°C\):
\[m_{H_20} = 18 \times \frac{0.21 \times 101325 }{8.314 \times (273.15 + 20)} = 157g\]Les gaz sont une des formes dans lesquels les molécules se trouvent. Il y a les solides, les liquides, et les plasmas et autres états indéfinis.
En chimie, on est souvent habitué au diagramme de phase, où étant donné une pression et une température, on connaît dans quel état se trouve (majoritairement) la matière. A titre d’exemple, à pression atmosphérique et -1°C, l’eau est sous forme solide (hors état de surfusion); à 20°C, l’eau est sous forme liquide, et à 110°C sous forme gazeuse.
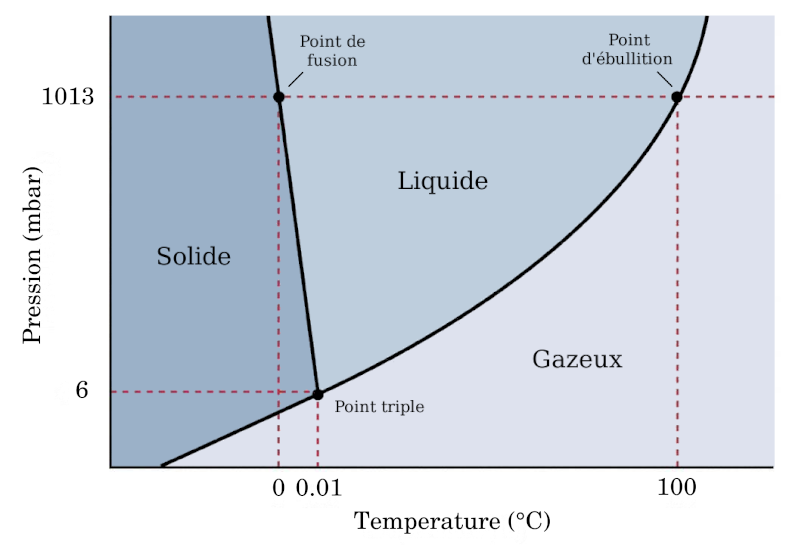
Source de l’image: Wikipedia
“Oui mais”, pas tout à fait. C’est la qu’intervient la loi de Raoult. En fait, lorsque l’eau est sous forme liquide, une partie est sous forme gazeuse, on a un équilibre. Quand on regarde le diagramme de phase, l’eau est liquide à pression atmosphérique. Mais si l’on met de l’eau dans un compartiment vide, c’est à dire à pression $P=0$, on n’est plus dans les conditions énoncées précédemment.
La pression à la surface du liquide est la même que dans l’air à la surface. L’eau liquide va alors se vaporiser, ce qui va avoir pour conséquence d’augmenter la pression et atteindre un équilibre.
La loi de Raoult donne une relation entre la proportion d’une molécule à l’état liquide, et sa proportion (pression partielle) à l’état gazeux. Elle régit les équilibre liquide-vapeur, et s’énonce de la manière suivante:
\[P_{i} = x_i P_i^{sat}\]où:
L’eau à l’état liquide est très souvent majoritairement composée d’eau (ça peut sembler évident). Même si vous considérer l’eau de mer, à 35g / L, en proportion, vous avez (en s’affranchissant de la conversion litres - kilo):
\[n_{H_2O} = (1000-35) / 18 = 53.6 mol\] \[n_{NaCl} = 35 / (58.5) = 0.6 mol\] \[\frac{n_{H_20}}{n_{H_2O} + n_{NaCl}} = \frac{53.6}{53.6+0.6} \approx 99\%\]Donc, la pression partielle de l’eau est égale à la pression de vapeur saturante à l’équilibre.
La valeur \(P_i^{sat}\) dépend du composé et de la température. Il existe différents modèles pour approximer cette valeur. Wikipedia en liste plusieurs.
Pour la simplicité, on va s’intéresser au modèle de Rankine, qui décrit l’évolution de la pression de vapeur saturante comme:
\[P^{sat} = P_0 \times \exp\left(13.7 - \frac{5120}{T}\right)\]A \(0°C\), la pression de vapeur saturante est de \(P^{sat}_{H_2O}(0°C) \approx 653 \approx 0.6\% P_0\)
Donc, si on avait une boite fermée, isotherme, à initialement 1 bar, dans laquelle on ferait bouillir de l’eau, techniquement, on pourrait augmenter la pression à 2 bars. Cependant, nous ne sommes jamais dans ces conditions extrêmes (système fermé), l’air circule, donc nous somme rarement à 4% d’eau dans l’air.
Avec tous ces éléments, on peut calculer la quantité d’eau maximale que peut contenir \(1m^3\) d’air. Il suffit de remplacer dans la loi des gaz parfait \(P\) par \(P^{sat}_{H_2O}\):
\[m_{H_20} = M_{H_20} n_{H_20} = M_{H_20} \left(\frac{P_{H_20}V}{RT}\right)\]On obtient cette courbe, dont quelques valeurs sont reprises dans la table:
| Temperature (en °C) | Eau liquide (en g) |
|---|---|
| 0 | 5 |
| 10 | 10 |
| 20 | 17 |
| 30 | 30 |
| 40 | 49 |
| 50 | 80 |
| 60 | 124 |
| 70 | 188 |
| 80 | 280 |
| 90 | 405 |
| 100 | 576 |
La température est perçu différemment en fonction de l’humidité. On parle souvent de “température ressentie”, et certaine plage d’humidité engendre une sensation d’inconfort.
La définition de l’humidité vient tout naturellement: c’est le ratio entre la pression partielle de la molécule considérée en phase gazeuse par rapport à la pression maximale (c’est à dire de saturation):
\[\text{Humidité} = \frac{P_{H_2O}}{P^{sat}_{H_2O}}\]La loi de Raoult nous disait que la pression partielle de l’eau est égal à sa pression de vapeur saturante à l’équilibre. Or, l’équilibre n’est pas instantané, il faut un certain temps avant que la pression effective soit égale à la pression maximale.
Il y a des manières de calculer la température ressentie en fonction de la température. Mais globalement, plus il fait humide, plus il semble faire chaud.
A cela s’ajoute aussi le vent: le vent a l’effet inverse. Plus il y a de vent, plus il semble faire froid.
Une simple illustration est la différence entre un 40°C au Maroc et un 40°C au Japon: au Maroc, l’air est plutôt sec, ce qui est supportable, alors qu’au Japon l’air est très humide en été. Ou encore la différence entre le sauna et le hammam:
Dans une maison, il y a différentes sources d’humidité:
Tout ces activitées augmentent la teneur en eau dand l’air, et entraîne des sensations d’inconfort.
Dans une maison, un taux entre 40% et 70% est recommandé. Néanmoins, pour conserver certains objets, il est préférable d’avoir des variations faibles (par exemple pour le bois, les pianos), où une fourchette restreinte (par exemple, les manteaux en fourrure où une humidité entre 45 et 55% est recommandée).
De plus, si l’air est trop chargé en eau, il peut y avoir de la condensation qui peut entraîner des moisissures et dégrader la qualité de l’air. Aussi, le séchage du linge est impactée si l’air est à saturation.
Les humidités à différentes température ne se valent pas. Si il fait 15°C dehors, qu’il pleut des cordes (humidité \(\approx 100 \%\)), vous n’aurez pas \(100\%\) d’humidité si votre pièce est à 20°C.
Supposons qu’il fait 20°C dans votre habitat, et que vous aérez pendant quelques minutes pour renouveler l’air. On suppose que le temps d’aération est trop court pour modifier la température de vos murs, si bien que quelques minutes après avoir fermé vos fenêtres, l’air est de nouveau à la température de 20°C.
L’exercice consiste à recalculer l’humidité d’un gaz après échauffement. En supposant que l’air extérieur est saturée (pluie torrentielle), on a:
| T°C | 0°C | 5°C | 10°C | 15°C | 20°C |
|---|---|---|---|---|---|
| eau/m3 | 5.2 | 7.1 | 9.7 | 13.0 | 17.3 |
| Humidité | 30% | 43% | 57% | 76% | 100% |
Donc si il fait 10°C dehors, avec une pluie torrentielle, mais que l’humidité interne est de 80%, mieux vaut aérer, on y est gagnant. Par contre, il n’est pas conseiller d’aérer s’il fait chaud et humide. En été, il est plutôt conseillé d’aérer le matin pour capter la fraîcheur, obtenir de l’air contenant moins d’eau, et par question d’hygiène.
En chimie, deux concepts cohabitent ensembles:
Si on prend la loi de Dalton, qui dit qu’il y a un équilibre entre la quantité d’un composant en phase liquide et celle en phase gazeuse, c’est une loi thermodynamique. Si l’équilibre était instantané, on aurait 100% d’humidité dans l’air, étant donné la quantité d’eau disponible dans les océans. Or, nous obtenons des valeurs d’humidité variables. L’équilibre n’est pas atteint immédiatement. Pour obtenir l’équilibre, il faudrait attendre encore et encore, sans jamais perturber le système. Or, la Terre tourne, une face chauffe quand l’autre se refroidit, bref c’est compliqué d’avoir les paramètres du système inchangés au cours du temps.
La cinétique est la pour répondre à ses questions de transition. Les mécanismes qui permettent d’homogénéiser la température d’un gaz sont la conduction et la convection. La conduction est la diffusion de la chaleur sans mouvement de masse. C’est la loi de Fick. La convection fait appel au mouvement des masses, qui vont se mélanger progressivement pour avoir des caractéristiques (temperature, pression, composition) homogènes sur un volume continu.
Lorsque l’on fait chauffer de l’eau dans une casserole, l’eau chaude va chauffer localement l’air au dessus de la casserole. Cette augmentation de la température va permettre de stocker plus d’eau à l’état gazeux (évolution de $P^{sat}$). L’eau se vaporise donc. Cependant, l’air de la pièce lui n’est pas de même concentration en eau, ni de même température. Il va donc y avoir un phénomène de convection de l’air chaud et humide vers le reste de la pièce. L’air au dessus de la casserole s’appauvrissant, de l’eau supplémentaire est évaporée.
Dans une cuisine de \(10m^2\), et 2.5m sous plafond (\(25m^3\)), on peut stocker à 20°C \(25 \times 17.3 = 430g\) d’eau, ce qui n’est pas assez pour contenir l’eau entière d’une casserole de pâte (1L d’eau pour 100g de pâtes). Du coup, il est possible d’arriver à saturation (humidité de 100%).
Le rôle du couvercle est de bloquer ce déplacement d’air. Cela évite de perdre toute l’eau. Evidemment, le couvercle n’est pas étanche, mais ça limite déjà énormément.
Le couvercle n’isole pas complètement. En effet, l’air de la pièce sec se réchauffe au contact du couvercle et de la casserole, donc il reste des pertes d’énergie.
Avec ou sans couvercle, il y a convection de l’air qui refroidit la casserole. Donc ça peut sembler presque équivalent d’un point de vue énergétique. Néanmoins, un deuxième point à considérer est le coût énergétique du changement d’état de l’eau. Le passage de l’eau de l’état liquide à gazeux coûte de énormément d’énergie. L’enthalpie de vaporisation est de \(\Delta H_{l \rightarrow v} = 2 257 kJ/kg\) (ça fait juste beaucoup …). Certes, vous chauffez votre pièce avec cette eau chaude sous forme vapeur, mais l’air humide n’est pas confortable … En piégeant l’air saturé en eau, vous évitez de faire évaporer de l’eau pour rien.
Donc, en résumé, le couvercle permet d’éviter:
Beaucoup de personnes ignorantes se laissent avoir par les complotistes (souvent ignorants eux aussi). Un des meilleurs gags complotistes est celui des traces d’avions. Quelqu’un me disait:
“En France, à chaque fois que je vois un avion, il y a une trace blanche derrière, alors que en Allemagne, rien. On nous balance des produits chimiques sur la tête.”
Alors certes, il y a des nano-technologies qui permettent de déclencher des averses. Le problème de “France” et “Allemagne” n’a rien à faire dans l’histoire. La personne ne se trouve juste pas à la même distance de l’aéroport dans ces deux endroits.
Si vous observez bien les avions, ce sont les avions “très haut” qui font ces traces. Les avions en phase d’atterrissage n’en font jamais. Les avions, en période de croisière, vole vers 7.000 m d’altitude. A cette altitude, il fait froid (montez sur l’Everest et vous verrez). A cette température, la pression de vapeur saturante est très faible, et il n’y a quasiment pas d’eau dans l’air.
Cependant, certains moteurs dégagent de l’eau (sous forme de vapeur). Cette vapeur chaude est éjectée des moteurs, et se refroidit très vite en partant de l’avion. En refroidissant, l’air arrive à saturation, et ne peut conserver toute cette eau. L’eau gazeuse se transforme en liquide, puis en glace, devenant opaque à l’oeil, ce qui explique ces traînées.
>> You can subscribe to my mailing list here for a monthly update. <<