MinHash is a simple algorithm allowing to compute probabilistically the similarity of two set A and B according to the Jaccard similarity coefficient.

J(A, B) = \frac{|A \cap B|}{|A \cup B|}

The two extreme values are 0 (no value in common) and 1 (the two set contains the same elements).

Naive case

In the classical case, if you want to know which is the similarity between two sets of n and m elements, in the worst case, where you compare each element to each others, you need to do n * m comparisons. You can improve this number by sorting elements, and other tricks.

If elements are not "simple" as float, characters or boolean values, like strings or multidimentional objects, the number of comparison can be very high.

Issues

• Problems with highly dimensional values and their comparison
• Projecting into a hash space allow easy to manipulate objects

Cost and complexity

Cost_K be the cost to compare two elements.

Two choices for exact calculation:

• Compare all non sorted elements together Cost_K(n * m)

• Sort the two sets and compare each ordered set together Cost_K(nlogn + mlogm + max(n, m)) ≤ Cost_Kmax(n, m)(1 + log(max(n, m)))

Graphical representation

Variant with multiple hash functions

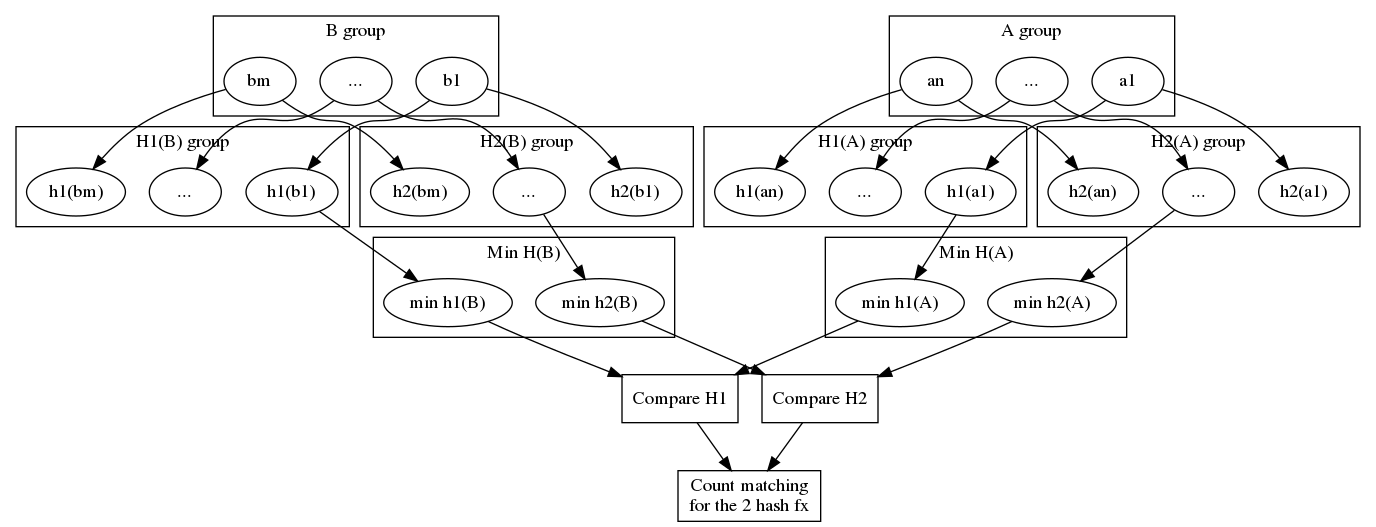
Be K the object space, A and B two set of n and m elements respectively with value in K. Be H the set of j hashing functions, with jinf min(n, m).

A = {a_i ∈ K|i ∈ [1, n]}

B = {b_i ∈ K|i ∈ [1, m]}

H = {h_i|i ∈ [1, j]}, H : K ↦ R

For all elements of A and B, we compute all the H hash function over all elements, and keep for each set the minimal values founds. This require n * j and m * j operation for each set, plus sorting the value, that can be done in j * nlog(n) and j * mlog(m).

After keeping the smallest values for each hashing function of both set, all j pair of values are compared, leading to j comparison only.

The Jaccard coefficient can be approximed as

J(A, B) \simeq \frac{|\{min(h_i(A))= min(h_i(B))| i \in [1, j]\}|}{j}

Operation cost

Defining Cost(h) the cost for computing the hash function over an object of K, and Cost(cmp) the cost for comparing two hash values, under the hypothesis that all hash values have the same comparison cost, the number of operation can be summarized as :

j * Cost(h)*(n + m)+j * Cost(cmp)*(nlog(n)+mlog(m)+1)≤2 * p * j * (Cost_h + Cost_cmp * log(p)) + j * Cost_cmp with p = min(m, n)

Graphical representation

Example with two set A and B with 2 hash functions.

Errors of computation and validity given size and cost parameters

Hash collisions

Variant with single hash function

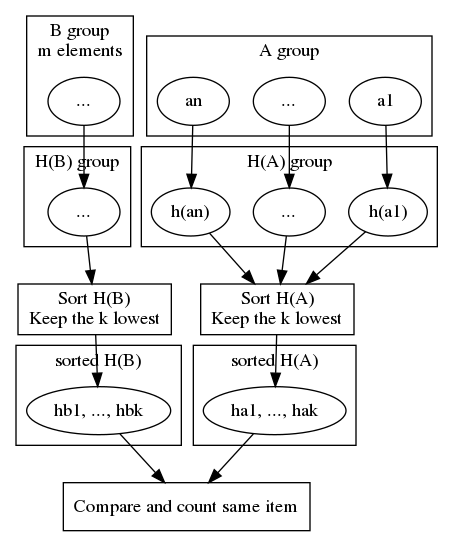
Instead of using multiple hash functions, we use only one, and rank hashed values.

Be h : K ↦ R

Calculate H(A)={h(a)|∀a ∈ A} Sort H(A) and keep the k lowest values H(A)_k = {h(a_i)|i ∈ [1, k − 1],h(a_i)≤h(a_i + 1)} Do the same for B and compare elements of each hash value sets together.

Cost

For this variant, it cannot be calculated with k comparisons, as values are all in the same space. The comparison has to be made using exact techniques, with 2k comparisons, which is still very good (as values are already sorted).

Cost_h(n + m)+Cost_cmp(nlogn + mlogm + 2k)

Graphical representation